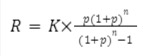Program Pierwsze Mieszkanie – nowy program rządowy

Program Pierwsze Mieszkanie ma się składać się z dwóch rozwiązań

Pierwsze rozwiązanie to: Bezpieczny Kredyt 2%, czyli system dopłat do kredytu na zakup pierwszego M.

Drugie to Konto Mieszkaniowe – program pomoc oszczędzającym na zakup pierwszego mieszkania.

Oba instrumenty mają być kompleksowym rozwiązaniem dla osób, które chcą kupić pierwsze mieszkanie, lub planują to w perspektywie następnych kilku lat.

Niestety informacje przedstawione na stronie rządowej, nie są zbyt szczegółowe, przedstawiają raczej ogólną wizję programu. 

Z przekazów medialnych przedstawicieli resortu Ministerstwa Rozwoju będzie można łączyć „Program Pierwsze Mieszkanie” i „Mieszkanie bez wkładu własnego”.

• Kredytobiorca do 45 roku życia
• Kredytobiorca, który nie ma i nie miał mieszkania/domu na własność
• Kredytobiorca, który nie ma i nie miał spółdzielczego prawa do lokalu lub domu
• Brak limitu ceny zakupu

• 500 tys. zł. – maksymalna wysokość kredytu, który może uzyskać 1 osoba,
• 600 tys. zł. – maksymalna wysokość kredytu, który może uzyskać małżeństwo lub  rodzice z dzieckiem,
• Kredyt można otrzymać na mieszkanie z rynku pierwotnego i wtórnego oraz na zakup lub budowę domu, jego wykończenie, a także na zakup działki budowlanej,
• Brak limitu ceny za 1 m2.

• W okresie stosowania dopłat (pierwsze 10 lat spłaty kredytu) oprocentowanie kredytu wyniesie dla kredytobiorcy 2%. Oprocentowanie to zostanie powiększone o marżę i prowizję  banku, jeśli będzie pobierana,
• Wsparcie będzie przewidziane dla kredytów o okresowo stałej stopie procentowej,
• W okresie stosowania dopłat do rat tego kredytu (pierwsze 10 lat spłaty) efektywne oprocentowanie kredytu z perspektywy kredytobiorcy wyniesie 2% + marża banku,
• Przez pierwszych 10 lat kredyt będzie spłacany w systemie rat malejących, natomiast po tym czasie w równych.

O różnicach pomiędzy ratą równa a ratą malejącą oraz sposobie liczenia pisałem w tym artykule. 

Jeżeli chodzi o posiadanie innych nieruchomości to z Q&A z przedstawicielem ministerstwa wynika, że z tej reguły mają być wyłączone  udziały w nieruchomościach nabyte na podstawie dziedziczenia i pod warunkiem niezamieszkiwania w tych nieruchomościach.

Z wypowiedzi medialnych wynika, że kredyt ma być oprocentowany stałą stopą procentową. Raty będą spłacane w systemie malejącym w okresie dopłaty. Po okresie dopłaty klienci będą spłacać kredyt w ratach równych. O rodzajach rat pisałem tutaj. 

Dobrą informacją jest też to, że KNF ma obniżyć regułę ostrożnościową tzw. bufor,  zdolności kredytowej z obecnego 5% do 2,5%.   Reguła ostrożnościowa – bufor, polega na tym, że licząc zdolność kredytowa klienta bank do oprocentowania kredytu, dodaje obecnie 5%. Jeżeli z tym powiększonym oprocentowaniem klient ma zdolność kredytową to bank, wyda klientowi pozytywną decyzję kredytową.  Dla przykładu, jeżeli wg oferty banku oprocentowanie kredytu wynosi 7,75% w skali roku, to do policzenia zdolności kredytowej klienta bank przyjmie oprocentowanie 7,75%+5% = 12,75%. Po obniżeniu reguły oszczędnościowej będzie to 10,25%. Pozwoli to na zwiększenie zdolności kredytowej potencjalnych klientów. O zdolności kredytowej pisałem w poniższym artykule. 

Jeżeli chodzi o procedurę udzielania kredytu „Bezpieczny Kredyt 2%”, ma być taka sama jak w przypadku zwykłego kredytu hipotecznego.  Kredytobiorca składa wniosek o kredyt u pośrednika kredytowego lub w banku, który przystąpił do programu.  Kredytobiorcy będą przedstawione dwie oferty: oferta rynkowa i oferta „bezpieczny kredyt 2%”.  Współpraca pomiędzy bankiem kredytującym klienta a Bankiem Gospodarstwa Krajowego i sam system dopłat ma być dla kredytobiorcy nieodczuwalny. 

Założenia: 

• Kwota kredytu 400.000,
• Okres 20 lat – 240 miesięcy,
• Oprocentowanie rynkowe z marżą 8,46%,
• Oprocentowanie z dopłatą 2,85%,
• Pierwsza rata bez dopłaty 4.486,67,
• Pierwsza rata po dopłacie 2.615,33,
• Rata po 10 latach 2.475,44.

Obliczenia dotyczące przykładu 1 opisałem na końcu wpisu w rozdziale pt.: „Obliczenia dla przykładu pierwszego”

Kredytobiorca, zaciągając kredyt w wysokości 400.000 na okres 20 lat, w Programie Bezpieczny Kredyt 2%  zaoszczędzi na oprocentowaniu 168 888,13, w porównaniu z kredytem w takiej samej wysokości na warunkach rynkowych.  Warto też zwrócić uwagę, że przy tym okresie kredytowania po 10 latach kredytobiorca spłaci połowę swojego kredytu.

• Kwota kredytu 300.000,
• Okres 25 lat – 300 miesięcy,
• Oprocentowanie rynkowe z marżą 8,46%,
• Oprocentowanie z dopłatą 2,85%,
• Pierwsza rata bez dopłaty 3.115,00,
• Pierwsza rata po dopłacie 1.711,50,
• Rata po 10 latach 1.768,31.

Kredytobiorca, zaciągając kredyt w wysokości 300.000, na okres 30 lat, w Programie Bezpieczny Kredyt 2%  zaoszczędzi na oprocentowaniu 135.016,70, w porównaniu z kredytem w takiej samej wysokości na warunkach rynkowych.

• Kwota kredytu 350.000,
• Okres 30 lat – 360 miesięcy,
• Oprocentowanie rynkowe z marżą 8,46%,
• Oprocentowanie z dopłatą 2,85%,
• Pierwsza rata bez dopłaty 3.439,72,
• Pierwsza rata po dopłacie 1.802,31,
• Rata po 10 latach 2.019,02.

Kredytobiorca, zaciągając kredyt w wysokości 350.000, na okres 30 lat, w Programie Bezpieczny Kredyt 2%  zaoszczędzi na oprocentowaniu 164.014,12 w porównaniu z kredytem w takiej samej wysokości na warunkach rynkowych.

• Kwota kredytu 550.000,
• Okres 30 lat – 360 miesięcy,
• Oprocentowanie rynkowe z marżą 8,46%,
• Oprocentowanie z dopłatą 2,85%,
• Pierwsza rata bez dopłaty 5.405,28
• Pierwsza rata po dopłacie 2.832,19
• Rata po 10 latach 3.172,74

Kredytobiorca, zaciągając kredyt w wysokości 550.000, na okres 30 lat, w Programie Bezpieczny Kredyt 2%  zaoszczędzi na oprocentowaniu  257 737,63 w porównaniu z kredytem w takiej samej wysokości na warunkach rynkowych.

Drugie rozwiązanie to specjalne konto oszczędnościowe, prowadzone przez banki komercyjne. Będzie je mogła otworzyć osoba, która nie ma i nie miała mieszkania. (w tym domu jednorodzinnego lub spółdzielczego prawa dotyczącego lokalu mieszkalnego albo domu jednorodzinnego). Z programu może skorzystać także osoba, która w jednym posiadanym niewielkim lokalu mieszka z co najmniej dwójką własnych lub przysposobionych dzieci. (lokalu o pow. do 50 m2 przy dwójce dzieci, 75 m2 przy 3 dzieci i 90 m2 przy 4, bez limitu m2 przy 5 i większej liczbie dzieci). https://www.gov.pl/web/rozwoj-technologia/pierwsze-mieszkanie

• Wiek wejścia od 13 do 45 lat
• Okres oszczędzania na koncie wynosi od 3 do 10 lat.
• Systematyczne wpłaty od 200 do 2000 miesięcznie (co najmniej 11 wpłat rocznie)
• Premia Mieszkaniowa z Banku Gospodarstwa Krajowego: równa rocznemu wskaźnikowi inflacji lub wskaźnikowi wzrostu cen mieszkań (naliczany będzie wyższy wskaźnik)  –  naliczana corocznie, wypłacana jednorazowo.
• Zgromadzone środki wraz z premią można będzie wydać na zakup pierwszego mieszkania, domu lub wkład finansowy w inwestycję, np. w ramach spółdzielni mieszkaniowej.
• W przypadku zakończenia oszczędzania, na wydanie środków będzie 5 lat.

Z informacji medialnych wynika, że Konto Mieszkaniowe może być zakładane dla dzieci, które skończyły 13 roku życia.   

Miesięczna wpłata pomiędzy 500-2000. Co miesiąc będzie można wpłacać inną kwotę pod warunkiem, że będzie mieściła się w przedziale.  Raz do roku będzie można zaniechać jednej wpłaty.

Gromadzone środki będą  oprocentowane wg oferty banku, w którym jest założone konto oszczędnościowe i co roku będzie dopisywana premia z BGK. Wysokość premii to wskaźnik inflacji lub wskaźnika wzrostu cen nieruchomości. BGK dopisze większy ze wskaźników. Po skończeniu okresu oszczędzania klient będzie miał 5 lat na przeznaczanie zgromadzonych środków na cel mieszkaniowy. 

Z przekazów medialnych wynika również że lokata będzie zwolniona z tzw.  podatku Belki

W prezentacji ministerstwa podany jest przykład regularnego oszczędzania przez okres 3 lat i miesięcznych  wpłatach w wysokości 1.000,00.  Wynika z niego, że premia będzie, naliczana wg procentu składanego.  Premia będzie naliczana co miesiąc od bieżącej wysokości lokaty w pierwszym miesiącu od: 1.000,00 w drugim miesiącu od: 2.000,00 i tak dalej. 

Z prezentacji wynika, że przy takich założeniach, po roku oszczędzania Premia Mieszkaniowa wyniesie: 624,00 a po 3 latach: 5.328,00.  Do tego jeszcze dojdą odsetki od banku.

Sprawdziłem te wyliczenia w następujący sposób.

Roczny wskaźnik inflacji podzieliłem na 12, aby otrzymać wskaźnik miesięczny.

Inflacja roczna 9,6%/12 = 0,008.

Comiesięczny stan lokaty mnożyłem tym wskaźnikiem i na koniec podsumowałem. Wynik wyszedł dokładnie tak jak w prezentacji rządowej.

Mając już gotowe narzędzie, postanowiłem sprawdzić, jak będzie premia po 10 latach przy maksymalnej wpłacie 2.000,00 miesięcznie i przy złożeniu inflacji na poziomie 9,60%

Z moich wyliczeń wynika, że po 10 latach oszczędzania i regularnych wpłatach 2.000 miesięcznie Premia Mieszkaniowa wyniesie 113. 232,00 a zgromadzony kapitał 240.000.  PO 10 latach, klient będzie dysponował łącznym kapitałem: 353.232,00.  Do tego trzeba jeszcze doliczyć odsetki bankowe.

Niestety aktualnie nie znalazłem oferty banku, która mogłaby być dedykowana do programu.  Dlatego zaniechałem tych wyliczeń.  Jak tylko pomysł rządowy zostanie przekuty w rozwiązania prawne i banki przygotują odpowiednią ofertę, uzupełnię moje wyliczania.

Spłata kredytu ma następować w ratach malejących, które liczy się w następujący sposób:

Kwotę, która pożyczamy, dzielimy przez okres kredytowania w miesiącach: 400.000/240=1666,67.  Otrzymujemy część kapitałową każdej z 240 rat.  Tyle miesięcznie będziemy spłacać z kwoty, która pożyczyliśmy.

Cześć odsetkowa (zarobek banku) liczymy w następujący sposób: saldo do spłaty *oprocentowanie roczne/12 (oby policzyć oprocentowanie miesięczne): 400.000*0,705% (8,46%/12 = 0,705%) = 2820 i to jest część odsetkowa w pierwszej racie.

Czyli pierwsza rata bez dopłaty rządowej wynosi: część kapitałowa + część odsetkowa = rata 4.486,67 (czyli tyle ile podaje prezentacja rządowa).

Teraz pierwsza rata z dopłatą rządową.  Skoro wiemy, że cała rata wynosi: 2.615,33, a część kapitałowa 1.666,67 to część odsetkowa, będzie wynosiła: 948,66.  Dopłata z BGK wyniesie zatem 718,01 w pierwszej racie. Czy to jest 2%?  Przekształcę zatem wzór na część odsetkową w racie: 400.000 * X% = 948,66 X% = 948,66/400000 = 0,00237%.  Wynik to t oprocentowanie miesięczne, więc mnożymy *12, aby otrzymać oprocentowanie roczne. 0,0284598 i mnożymy *100, aby otrzymać wartość % = 2,85%.  Jeszcze sprawdzenie 400.000*2,85%/12 = 948,66. (liczyłem przy użyciu Excela, na zwykłych kalkulatora są minimalne rozbieżności, ze względu na zaokrąglenia). Moje wyliczenia są zatem zgodne z prezentacją.  Z tych wyliczeń wynika, że „średnia marża” zastała określona na poziomie 0,85%.

Po 10 latach, czyli w 121 racie następuje zmiana z raty malejącej na ratę równą.  Przy oprocentowaniu 8,46% (założenia niezmienności) 121 rata wg. prezentacji rządowej, ma wynosić: 2.475,44.  Po 10 latach saldo kredytobiorca spłaci  1666,67*120 = 200.000,00. (obliczono w Excelu, na zwykłym kalkulatorze wychodzi minimalna różnica ze względu na zaokrąglenia).

Skoro mamy wysokość kredytu w 121 racie w wysokości 200.000, to możemy policzyć ratę wg oprocentowania 8,46%.

Wzór na obliczenie raty równej:

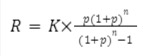
R – rata
K – kwota kredytu
p – wysokość oprocentowania kredytu (dla jednego okresu n, czyli w tym przypadku 1 miesiąca)
n – liczba rat.

W pierwszej kolejności obliczamy parametr p, czyli procentowanie w skali miesiąca:

Oprocentowanie w skali roku /12 = 8,46%/12 = 0,00705

Następnie obliczamy (1+p)ⁿ, a więc (1+0,00705) do potęgi 120, oznaczającej okres kredytowania wyrażony w miesiącach: 2,3234

Dzięki powyższym obliczeniom udało się ustalić wartości występujące we wzorze, które następnie do niego podstawiamy:

K – 200 000 PLN
p – 0,00705
n – 120
(1+p)ⁿ – 2,3234

Po podstawieniu do wzoru otrzymujemy ratę równą w wysokości 2475,44, czyli dokładnie tyle ile w prezentacji ministerstwa.

Wysokość raty równej można też policzyć na mojej stronie lub Excelu przy pomocy formuły PMT.

Skoro już wiemy, jak zostały policzone symulacje w prezentacji rządowej, sprawdźmy, jakie będą korzyści, dla kredytobiorcy.  Na podstawie własnych wyliczeń sporządziłem dwie symulacje, na takich samych warunkach oprocentowania, okresu kredytowania przy założeniu przejściu z rat malejących na równe po okresie 10 lat.